R’da ilk uygulama: Mandelbrot Fraktali

Nispeten, basit bir denklem setinin sonsuz karmaşık davranışlara yol açabileceği düşüncesi, matematiksel düşünen ve akademik insanların ötesinde ilgi çekicidir.

Fraktallar pop kültürün bir parçası haline geldi ve kaos fikri, “Kelebek Etkisi” terimi tarafından popüler hale getirildiği için matematiksel araştırmanın dışındakiler tarafından pek de bilinmemektedir (Ancak, ne yazık ki Ashton Kutcher’ın başrol oynadığı filmin bu konuyu tam olarak açıkladığını da söyleyemem).

Doktora eğitimime başladığım andan itibaren, fraktallar ve kaosla çok ilgilendim. Bu ilgiyi gerçekten teşvik eden şey, “kaosun matematiği” nin tarihini oldukça okunabilir şekliyle özetleyen James Gleick’in Kaos‘uydu. Öyle ki, Doktora tezimi de bu konuda yazmaktayım.

Bu durumda, fraktallere R’de bir şans vermem gerektiğini düşündüm.

Mandelbrot Fraktali

Kuşkusuz, en iyi bilinen fraktal, Mandelbrot fraktalidir. Zahmetli matematiksel ayrıntılara girmeden, Mandelbrot kümesi, z = x + yi formundaki sayılar olan karmaşık sayıları kullanmaktan kaynaklanır.

i sayısı, “hayali birim” olup, i² = -1 olacak şekilde özel bir değerdir. Bu tür karmaşık sayılar benzersiz olduğundan, ikisini birlikte çarpmak, gerçek sayı doğrusundaki sayılardan çok farklı davranışlara neden olabilir: gerçek ve büyüklüğü 1’den büyük olan hayali parçaların, çarpılan terimlerden daha büyük olacağı garanti edilmez.

Mandelbrot, aşağıdakiler tarafından üretilen sayı kümesini düzenlemiştir:

1. Karmaşık düzlemde tümü z = 0 olan karmaşık bir sayılar kümesini başlatın.

2. Formülü itere edin

Z_n+1=(z_n)²+c

Bu formülde; c, karmaşık düzlemi dolduran bir dizi karmaşık sayıdır.

3. Mandelbrot kümesi, z’nin tüm n’ler için sınırlı kaldığı kümedir.

Ve matematiksel olarak, eğer iterasyon altında z, 2’den büyükse, kümede olmadığı gösterilebilir.

Pratikte kişi, belirli bir c için z’den ayrılması gereken yinelemelerin sayısını takip eder ve ardından noktaları buna göre “ıraksama hızlarına” göre renklendirir.

Uygulama

Faz uzayı için bazı parametreler seçelim (x ve y için aralık ve çözünürlük, yineleme sayısı, vb.) Ve ardından iterasyona başlayalım. Kodumuz, aşağıdaki şekliyle hazır:

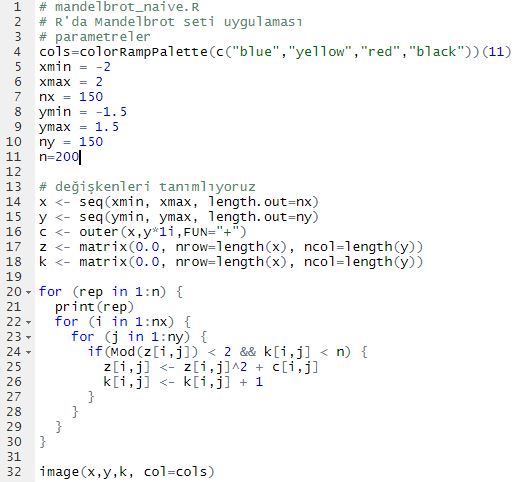
Son olarak, elde ettiğimiz çizime bakalım:

Tebrikler, ilk kodumuzu çalıştırdınız.